Lecture 15 of 18.
Rudolf Steiner, Stuttgart, January 15, 1921:
My Dear Friends,
Today I will deal with some of the things that may be causing you difficulty in understanding what we have done hitherto. I will lead over from these difficulties into a realm of ideas which will show up the inadequacy of those lines of thought on which the people of our time, with all their comfortable mental habits, would gladly found their understanding of universal phenomena.
Today I will deal with some of the things that may be causing you difficulty in understanding what we have done hitherto. I will lead over from these difficulties into a realm of ideas which will show up the inadequacy of those lines of thought on which the people of our time, with all their comfortable mental habits, would gladly found their understanding of universal phenomena.
We have been studying the universal phenomena in their relation to man. We have done so in manifold directions. Again and again we have indicated how a relationship reveals itself between the forming of man and what appears in the celestial phenomena. Whether we go by some ancient cosmic system or by the Copernican theories in forming our pictured synthesis of the movements of heavenly bodies, we must relate the picture to man — in diverse ways, of course. This we have seen. For a true science we must accept that there is this relation.
Yet the difficulties are formidable. Earlier in these lectures we drew attention to one such difficulty. The moment we try to form ratios between the periods of revolution of the planets of our system we come to incommensurable numbers. Arithmetic runs out, as we might say; we get no farther with it, for where incommensurable numbers enter in there is no palpable unit. Thus, when we look for a synthesis of the phenomena of cosmic space with our accustomed mathematical method and way of thinking, the phenomena themselves are such that we find ourselves driven farther and farther from reality. We may not therefore take for granted that we shall ever be able to explain the cosmic phenomena on the accustomed basis of our geometry, that is to say, within a rigid three-dimensional space. Nay more, another difficulty has emerged. Yesterday we found ourselves obliged to assume a certain relationship of Sun and Moon and Earth, finding expression in some way in man — in man's very structure. We would fain grasp how the relation is. Yet if we posit this working-together of the Three [Sun, Moon, Earth] we get into formidable difficulties in spatial calculation.
All these things we have mentioned. Now we can reach a certain starting point at least, through pure geometry — yet a geometry of a higher kind. Thence we may gain an idea of where the difficulties come from when we are trying by dint of spatial calculation to grasp the interconnection of celestial phenomena. Let us recall our previous attempts to comprehend the form of man himself. We are then let to this:- We can and we should try to take seriously that 'memberment' of the human being of which we have also spoken in these lectures. The human head-organization, we may truly say, centering as it does in the nerves-and-senses system, is relatively independent. So is the rhythmic system with all that belongs to it. So also is the metabolic system, and all that goes with it. In the human organization three independent systems are revealed. Taking our start now in an intelligent way from the principle of metamorphosis, as we must always do when dealing with organic Nature, we can try to form ideas upon this question: How are the three members of the threefold human system related to each other, according to this principle of metamorphosis?
Understand me rightly, my dear friends. We want to gain an idea — though it be only pictorial to begin with — of how the three members of the human system are related to each other. On the face of it, it will of course be difficult. Such organs as are met with in the human head: it will be difficult to recognise in them at all clearly the metamorphosis of those organs which are fundamental to the metabolic and lymph system. But if we go into the morphology of man deeply enough, we can find our way. We only have to think most thoroughly along the lines already indicated — namely, the essence of the mutual relation of the long bone to the skull-bone and vice versa is a complete turning-inside-out. The inner surface of the bone becomes the one turned outward. It is the principle by which you turn a glove inside out, provided only that the turning-inside-out involves a simultaneous change in the inherent relationships of inner forces. If I should turn a tubular bone or long bone inside-out like a mere glove, I should again get the form of a tubular bone, needless to say. But it will not be so if we take our start, as we must do, from the inherent configuration of the bone. As I described before, in its inherent configuration the long bone is oriented inward towards the radial quality that runs right through it. It is obliged therefore to subject its material structure and arrangement to the radial principle. When I have "flipped" it, so that the inner side opens outside, in its configuration it will no longer follow the radial but the spheroidal principle. The "inner side", now turned outward towards the Sphere, will then receive this form: (Fig. 1)

Figure 1
What was outside before, is now inside, and vice versa. Take this into account for the extreme metamorphosis of tubular bone into skull-bone and you will say: The outermost ends of human memberment — lymph-system and skull system — represent opposite poles in man's organization. But we must not think of "opposite poles" in the mere trivial, linear sense of the word. In that we go from one pole to the other, we must adopt the transition which this involves, namely from Radius to surface of a Sphere. Without the help of such ideas and mental pictures, intricate as they may seem, it is quite impossible to gain a just or adequate notion of what the human body is.
We come now to what constitutes the middle, in a certain sense, — the middle member of man's organization. This will be all that belongs to the rhythmic system, and it will somehow form the transition from radial structure to spheroidal.
In the threefold system thus presented we have the key to the morphological understanding of the entire human organism. Of course we need to realise how it will be. Suppose we have some organ in the metabolic system — the liver, for example — or any one of the organs mainly assigned to the metabolism. (We must qualify it with the word 'mainly' for there is always an overlapping and interlocking of these things). Suppose then we begin with such an organ and seek what answers to it in the head. We try to find which of the organs in the head-nature of man may be connected with it by the metamorphosis of turning-inside-out. We shall then have to recognise the organ when entirely transformed, de-formed; only by so doing shall we understand it. It will therefore not be easy to take hold of mathematically. Yet without finding some mathematical way of access we shall never adequately grasp it. And if you call to mind (even if you only take this as a picture) — if you call to mind that the real understanding of the human form and figure will lead us out among the movements of celestial bodies, you will divine what must be needful also when we wish to comprehend the latter. For a true synthesis of the phenomena of movement among the heavenly bodies, it will be quite inadequate to think of them as if these movements were accessible to a geometry that simply reckons with ordinary rigid space and therefore cannot master the turning-inside-out. For when we speak of a turning-inside-out in the way we have been doing, we can no longer be thinking of ordinary space. Ordinary space holds good where we can calculate volumes, cubicle contents, in the conventional way. We cannot do so if obliged to make the inner outer. We can no longer go on calculating them with the same conceptions which hold good in ordinary space.
If then in thinking of the human form and figure I need the turnings-inside-out, in thinking of the movements of heavenly bodies I shall need them too. I cannot proceed like the current Astronomy which tries to comprehend the celestial phenomena within an ordinary rigid form of space.
Take, to begin with, simply the head-organization and the metabolic organization of man. To pass from one to the other you must imagine, once again, a turning-inside-out — and, what is more, one that involves variations of form. Let us at least try to get a picture of the kind of thinking involved. We did preliminary work in this direction when speaking of the Cassini curves, and of the circle differently conceived. Ordinarily the circle is defined as a curve all of whose points are equidistant from one central point. We were speaking of the circle as a curve, all of whose points are at measured distances from two fixed points, and so that the quotient of the two distances is constant. This was our other conception of the circle.
Speaking of the Cassini curve, we showed that it has three essential forms. One, not unlike an ellipse: — this form arose when the parameters of the curve bore a certain relation, the which we indicated. The second form was the lemniscate. The third form is that while in the idea of it — and also analytically — it is a single entity, to look at it, it is not. It has two branches (Fig. 2),
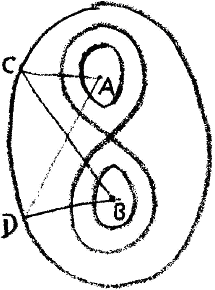
Figure 2
yet the two branches are one curve. To draw the line, we should somehow have to go out of space, coming back into space again when we draw the second branch. Conceptually, our hand would be drawing a continuous line when drawing the two regions which look separate. We cannot draw the line continuously within ordinary space, and yet conceptually what is here above and what is here below (the inner curve in Figure 2) is a single line. Now as I also mentioned, the same curve can be thought of in another way. You can ask what will be the path of a point which when illumined from a fixed point A appears with constant intensity of illumination, seen from another fixed point B. Answer: a Cassini curve. A Cassini curve will be the focus of all points through which a point must run, if when illumined from a fixed point A it is seen ever with the same intensity of light from another fixed point B (Fig. 2 again).
Now it will not be hard for you to imagine that if something shines from A to C (Fig. 2) and thence by reflection from C to B, the intensity of light will be the same as if reflected from D instead. But it gets rather more difficult to imagine when you come to the lemniscate. The ordinary geometrical constructions by the laws of reflection and so on will not be quite so easy to carry through. And it gets still more difficult to imagine with the two-branched curve, that the same intensity of light should always be observed from the point B, inside the one branch of the curve, when the original point-source of light is in A. You would have to imagine (as you pass from the one branch to the other) that the ray of light goes out of space and then shines into space again. You are up against the same difficulty as before, when you were simply asked to draw the two branches as one — with a single sweep of the hand through space.
Yet if we do not develop these conceptions we shall be unequal to the other task, namely of finding the transmutation — or even the mere relationship of form — as between any organ in the head of man and the corresponding organ in the metabolism. To find the connection you simply must go out of space. Once again — strange as it may sound — if with your understanding of any form in the human head you wish to make a transition to the understanding of a form in the human metabolic system, then you will not be able to remain in space. You must get out of space. You must get right out of yourself, looking for something that is not there in space. You will find something that is as little inside ordinary space as is what intervenes between the upper and lower branches of a two-branched Cassini curve. This is in fact only another way of expressing what was said before, that the metamorphosis must be so conceived as to turn the form completely inside out.
In thinking thus of the connection between the upper and lower branches of the discontinuous curve of Cassini (as shown in Fig. 3) we are still presupposing actual constants, rigid and unchanged, in the equation. Now if we vary the constants themselves as in an earlier lecture, forming equations of twofold variability, we shall be able to imagine the upper branch, say, in this form, and the lower one in this (Fig. 3).

Figure 3
The upper branch will take this form eventually. If then you alter the curve of Cassini by taking variables in place of constants — so that you start with equations instead of starting with invariable constants — you will get two different kinds of branches. Then there will also be the possibility for one of the two branches to come in as it were from the infinite and go out to the infinite again. This is precisely the relationship from which you should take your start when following certain forms within the human head, comprising them in curves and lines, and then relating them to the forms of organs or of complexes of organs in the metabolic system, which in their turn you will comprise in curves and lines. Such is the intricacy of the human form. To make it still less simple, you must imagine the one line (Fig. 3a) with an outward tendency, and the other with its tendency turned inward.

Figure 3a
You will be prone to say (I hope without insisting on it, but as a passing impression): If this be so, the human organization is so complicated that one would almost prefer to do without such understanding and fall back on the ordinary philistine idea of the body, as in the present-day Anatomy and Physiology. There we are not called upon to make such prodigious efforts as to let mental pictures vanish and yet again not vanish, or turn them inside-out, and all the rest! May be — but then you never really understand the human form; your understanding is, at most, illusionary.
Now, to go on: Suppose you thus look into it and recognize that there is something in the human organization which falls right out of space, is not in space at all, but obliges you for instance to imagine spatially separated line-systems, inherently united with each other and yet united by another principle than three-dimensional space affords. Thinking in this way, you will no longer be too far removed from what I shall now bring forward. You will at least be able to entertain the thought in a formal sense. No one, I mean, can validly object to thinking it as a pure form of thought. For to begin with, all we are called upon to do is to conceive a clear idea, as in mathematics generally. It cannot be objected that the thing is unproved, or the like. We are only concerned to reach a self-contained and consistent idea.
Think therefore for a moment that you had to do not only with ordinary space, conceived in its three dimensions, but with a "counter-space" or anti-space". Let me call it so for the moment, and I will try to evoke an idea of it, as follows. Suppose I form the thought of ordinary, three-dimensional, rigid space. I form the first dimension, I form the second dimension and I form the third dimension (Fig. 4).
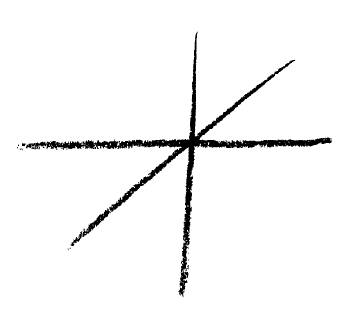
Figure 4
Then I have, so to speak, filled-in in thought — in the idea and mental presentation of it — three-dimensional space with which I am ordinarily confronted. Now as you know, in any such domain you can not only advance up to a certain degree of intensity; you can subtract from it too, and as you go on subtracting — taking away — you come at last to the negation of it. As you are well aware, there is not only wealth but debt. Likewise I cannot only make the three dimensions to arise in thought but I can also make them vanish. Only I now imagine the arising and vanishing to be a real process, — something that is really there. Of course it is possible to think only two dimensions instead of three, but that is not my meaning. What I now mean is this: The reason why I only have two dimensions (Fig. 4a)
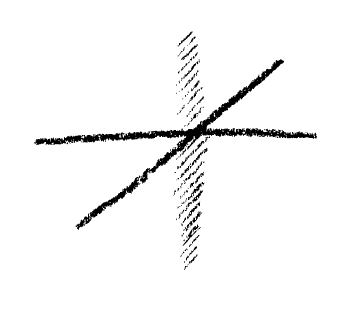
Figure 4a
is not that I never had a third. The reason is, I had a third and it has vanished. The two dimensions are an outcome of the coming-into being and vanishing-again of the third. I now have a space, which, though it outwardly shows only two dimensions, must inwardly be conceived as having two third dimensions, one positive and the other negative. The negative dimension springs from a source that can no longer be there in my three-dimensional space at all. Nor must I think of it as a "fourth dimension" in the conventional sense. No, I must think of it as being, to the third dimension, as positive to negative (Fig. 4a once more).
And now suppose that what I have been indicating is really there in the Universe; yet, as things generally are in the real world, approximately so. It would then be not a pedantically accurate but an approximate rendering of what I have here drawn. This need not cause you any great surprise, for in outer sense-perceptible reality you never find mathematical figures reproduced in any other way, always approximately. If then I claim that the picture represents something real, you will only expect it to do so in an approximate sense. To represent a reality corresponding to it, I need not repeat exactly the same drawing, but I should have to draw something flattened; that would answer to it. The fact that something has been there and has then vanished, I may perhaps suggest in this way: I will suppose that the density of an effect, indicated by the dark shading, came into being and then partly faded out again, drew weaker (Fig. 5).
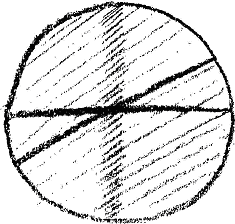
Figure 5
You are then left with a sphere that has a denser portion in the middle region. I beg you now, compare what is here drawn with the real cosmic system, such as we see it with our eyes, — the cosmic sphere with all the stars widely dispersed, and then the stars more densely packed in the region of the Milky Way, or what we call the Galactic System.
Yet you may also compare it with something else. Take any popular star-map. The picture we have shown (Fig. 5a)
Figure 5a
— let us still take it simply as a picture — is fundamentally equivalent to what is always being shown: the passage of the Sun or of the Earth through the Zodiac, with the North and South poles of the ecliptic somewhere out yonder. The idea we have been forming is, as you see, not so very remote from what is there in the outer Universe. In coming lectures we shall of course still have to look for more detailed relations.
Now for an understanding of what was said before about the human being we have not yet gone far enough. We must go farther and make the second dimension also vanish; so then we shall be left with only one, — with a straight line. But this is no ordinary straight line drawn into three-dimensional space. It is the line that has remained when we have made the third and also the second dimension vanish. And now we make the last remaining one to vanish. Then we are left with a mere point. Bear in mind however that we have arrived at the point by the successive vanishing of three dimensions. Now let us suppose that this point were to present itself to us in reality, — as having existence in itself. If it is there, and making itself felt, how then shall we imagine its activity? We cannot relate its activity to any point in the space determined by the x-axis. The x-axis is not there, since it has vanished. Nor can we relate it to anything with an x- and a y-coordinate, for all of this has gone; all this has vanished out of space. Nor can we relate it in its activity to the third dimension of space. What then shall we say? When it reveals its activity we shall have to relate it to what is quite outside three-dimensional space. Consistently with the procedure we have been through in our thinking, we cannot possibly relate it to anything that could still be included in this space. We can only relate it to what is outside three-dimensional space altogether. We can relate it neither to "x deleted" nor to "y deleted" not to "z deleted", but only to what deletes all three of them, z, y, and z together, and is therefore not within three-dimensional space at all.
We put this forward to begin with as a purely formal, mathematical notion. Yet is soon grows real. It grows exceedingly real when we begin to enter into things more deeply than with the easy-going notions with which science nowadays would gladly master them. Look, with this deeper tendency of understanding, — look at the process of sight and the whole organisation of the eye. You are perhaps aware (in other lectures I have often spoken of it) of how the eye is not merely to be regarded as a thing formed from within the body outward; for it is largely organized into the body from outside. You can trace the forming of it from without inward by studying the phylogenetic development of lower animals and then considering the act of sight itself. You will contrive to understand how the process of sight is stimulated from without and how the organ too is adapted to this stimulation from without. Then as the process works on inward to the optic nerve and farther in, it vanishes at length, — vanishes as it were into the organisation as a whole. I know you can find the termination of the optic nerves, and yet — this too comes to expression approximately — if you go into the inner organisation you will have to admit that it there vanishes.
So much for the process of sight and the associated organs. And now compare with this the process of secretion of the kidneys. Go into it conscientiously and you will have to relate the duct that leads outward, for the secretion of the kidneys, to what is working from without inward where the eye passes into the optic nerve. If you then look for ideas whereby the two things can be related, so that their mutual relation will help you understand the phenomena of either process, you will find indispensable such forms of thought as we have just been indicating. If you conceive the ideas of three-dimensional space as applying to the process of sight (we might also replace the one by the other), then, if you seek what answers to it in the secretion of the kidneys, you must realize that what is there enacted takes you right out of three-dimensional space. You must go through the same procedure in your thinking as I did just now in extinguishing the spatial dimensions. Otherwise you will not find your way.
In like manner you must proceed if you are trying to understand the curves formed in the Heavens by the apparent paths of Venus and Mercury on the one hand, Jupiter and Mars on the other, I mean quite simply the apparent paths as we observe them with our eyes, — the loops and all. If you use polar coordinates, for example, then for the loop of Venus you may make the origin of your coordinate system in three-dimensional space. Here you can do so. But you will not come to terms with reality if you adopt the same principle when examining the curve of Mars. In this case you must start from the ideal premise that the origins of any relevant system of polar coordinates will be outside three-dimensional space. You are obliged to take the coordinates in this way. In the former case you may start from the pole of the coordinate system, taking coordinates in the normal way, as in Figure 6.

Figure 6
But if you do this for the one planetary curve — say for the path of Venus with its loop — you will do equal justice to the paths of Jupiter or Mars with their loops only by saying to yourself: This time I will not pre-suppose a polar-coordinate system with an origin such that I always have to add a piece to get the polar-coordinates, as in Figure 6. No, I will take as origin of my polar-coordinate system the encompassing Sphere (Fig. 6a),
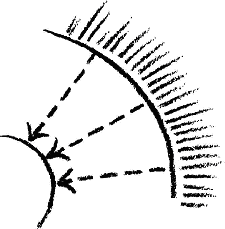
Figure 6a
i.e. what is there behind it, indeterminately far. Then I get such coordinates as these (dotted lines), where in each case, instead of adding, I must leave so much out. The curve I then obtain also has something like a centre, but the centre is in the infinite sphere.
It might prove necessary then, for more profound research into the paths of the planets, that we make use of this idea: In constituting the paths of the inner planets we must indeed attribute to these paths some centre or other within ordinary space. But if we want to think of centres for the path of Jupiter, the path of Mars, and so on, we must go right outside this ordinary space.
In fine, we have to overcome space; we must transcend it . There is no help for it. If you are conscientious in your efforts to comprehend the phenomena, the mere ideas of three-dimensional space will not suffice you. You must envisage the interplay of two kinds of space. One of them, with the ordinary three dimensions, may be conceived as issuing radially from a central point. The other, which is all the time annulling and extinguishing the first, may not be thought of as issuing from a point at all. It must be thought of as issuing from the encompassing Sphere — that is, the Sphere infinitely far away. While in the former case the "point" is of zero areas which it turns outward, and a point with the area of an infinite spherical surface which it turns inward. Geometrically it may suffice to conceive the notion of a point abstractly. In the realm of reality it will not. We shall not do justice to reality with the mere notion of an abstract point. In every instance we must ask whether the point we are conceiving has its curvature turned inward or outward; its field of influence will be according to this.
But you must think still farther, my dear friends; there is another thing. Of course you may imagine that you had somewhere caught this point which is really a Sphere. To begin with, since it is in the infinite far spaces you need not imagine it just here (s, Fig. 7). You can equally well imagine it a little farther out, (b, or c). You can imagine it to be anywhere out there; you only have to leave this sphere free (strongly drawn sphere in Fig. 7).
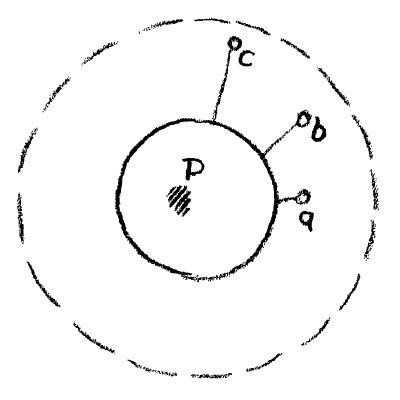
Figure 7
For this is hollowed out, so to speak; this is the inverted circle or the inverted sphere, if you like. But now suppose the following might be the case. Think of what is within this peculiar circle (namely at a, b, c, etc.). Think of this point that has its curvature turned inward. For in effect, the entire space outside this spherical surface is then a point with its curvature turned inward. And now imagine that this space had, after all, its limit somewhere. You might be able to go far away out, — very far. Suppose however the reality were such that you could not just go anywhere, but somewhere after all there was a limit of quite another kind (dotted circle in Figure 7). What there would appear, as if by inner necessity, what in effect belongs to the realm beyond the limit? An equivalent sphere would have to arise within, belonging to what is there outside. You would then have to realize: Out there, beyond a certain sphere, something is still existing, it is true, but if I want to see it I must look in here (P), for here it re-appears. The continuation of what is far away out there make itself felt in here. What I am looking for as I go out into infinite distances makes its appearance within, and becomes manifest to me from this centre.
These are the kinds of ideas you should develop to an adequate extent. In a formal sense they look sound enough. As forms of thought there can surely be no objection to them. Truly remarkable results will be obtained however, if with their help you try to penetrate outer reality. Think for example that there might be a phenomenon in celestial space, — we may call it "Moon" to begin with, — yet this phenomenon were not to be understood simply by saying: "This Moon is a body, here is its central point; we will investigate it on the understanding that it is a body and that its central point is here." Assume (and please forgive my saying, I put it euphemistically) assume that this way of thinking did not fit the reality, but that I ought to express it quite differently. I ought rather to say: "If I, in my Universe, start from a certain point and go farther and farther out, I come at length to where I shall no longer find heavenly bodies. Yet neither shall I find a mere empty Euclidean space. No, I shall find something the inherent reality of which obliges me to recognize the continuation of it here (at P)." I should then be obliged to conceive the space contained within the Moon as a portion of the entire Universe with the exception of all that exists by way of stars, etc., outside the Moon. I should have to think on the one hand of all the stars there are in cosmic space. These I am now assuming I have to treat in one way, according to a single principle; but the inside of the Moon — the space contained within the Moon — could not be treated in this way. It would require me to think as follows: There on the one hand I go out into the far spaces. Somewhere out there, I presume, is the celestial Sphere. Though it be only the "apparent" Sphere to begin with, something effective, something real, must be conceived to underlie it. Yet whatsoever realities I find out there, the space within the spherical surface of the Moon has nothing whatever to do with it. It only has to do with what begins where the stars come to an end. It is a fragment, in some strange way, belonging not to my Universe but to that Universe to which all the stars do not belong.
If there is such a thing within a Universe, it is a thing inserted in this Universe, occluded as it were, — a thing of altogether different nature and revealing different inner properties from all that is there around it. And we may then compare the relation of such Moon to its surrounding Heavens with the relation which obtains for instance between the secretions of the kidneys — with the organic structure that underlies them — and on the other hand the structure and functioning of the eyes. From this we shall proceed tomorrow.
It is not due to me that I must try to form, and to acquaint you with, such complicated notions of how the Universe is built. Truth is, equipped with any other notions you will not make headway, save on the convention: "Let us comprise the phenomena with our given range of ideas, and if we come to a limit somewhere, well then we do, and we go no further". Ascribe it then to the reality and not to any craving for remote ideas, if in the effort to impart an understanding of how the Universe is built I have unfolded complicated notions.



No comments:
Post a Comment